Stream ciphers, RC4 and biases

To just check out the JAVA-implemented RC4 cipher, have a look at the github repo.

Table of contents

Preamble

I’ve recently been keen on getting back into cryptography / cybersecurity topics to brush up on old knowledge from uni. One topic that’s come up when I’ve been browsing around is that of stream ciphers, i.e. ciphers where a continous stream plaintext digits are encoded with a keystream that has been generated with some key.

One of the arguably most famous stream ciphers is RC4 (Rivest Cipher 4) created by Ron Rivest, one of the co-creators of the RSA public key cryptography algorithm. This cipher ended up being used in protocols such as WEP, SSL (later TSL) and was kept as a trade secret of RSA Security for years, until it was reverse-engineered and posted on the Cypherpunks mailing list in September 1994.

In the wake of the cipher becoming public, researchers have identified a growing list of inherent issues and attack vectors in the algorithm. Consensus has grown over time among researchers that the RC4 cipher is considered unsafe, and in the latest version of TLS 1.3, the corresponding RFC 8446 (Rescorla, 2018)[^1]. states:

The security of RC4 cipher suites is considered insufficient for the reasons cited in [RFC7465]. Implementations MUST NOT offer or negotiate RC4 cipher suites for any version of TLS for any reason.

Although the cipher is now considered unsafe and is (hopefully) largely phased out, I still thought it would be interesting to get a basic understanding of its implementation as well as the identified issues, and so I decided to implement it.

RC4

As previously mentioned, stream ciphers are based on the notion of using a key to generate a keystream which is then combined with the plaintext to generate a cipherstream.

In RC4 the above operations are carried out as two main steps, KSA (Key-scheduling algorithm) and PRGA (Pseudo-random generation algorithm). A randomly generated key is used in the KSA to generate a permutation of all possible bytes S. This permutation is then used along with two pointers (i and j) to generate a keystream K of equal length to plaintext. The final cipher is then encrypted by outputting the XOR output of each byte-pair in the keystream and plaintext. Similarly, the cipher can be decrypted by XOR:ing the cyphertext against the keystream again.

Implementation

The following snippets are taken from the main class here here.

This is the key-scheduling algorithm. My approach was to stay clear of the byte type as much as possible, as the state array values need to be in the range[0, 255] and the java byte type is signed in the range [-128, 127], instead relying on the int type and converting any signed byte inputs into the unsigned range.

// Key-scheduling algorithm (KSA) returns the permutation **S**.
public int[] ksa() {
    // Note consistent usage of "int" over byte. byte is bounded -128 <= b <= 127
    // we need unsigned byte 0 <= b <= 255.
    int[] s = new int[256];
    // Initialize the original permutation of s (s[0] = 0, s[1] = 1, ..., s[255] = 255)
    for (int i = 0; i < 256; i++) {
        s[i] = i;
    }

    int j = 0;
    for (int i = 0; i < 256; i++) {
        j = (j + s[i] + this.key[i % this.keyLength]) % 256;
        int temp = s[i];
        s[i] = s[j];
        s[j] = temp;
    }

    return s;
}

Then follows the PRNG algorithm for achieving the intended keystream:

// Generates a pseudo-random keystream to be used in plaintext encryption
public int[] prng(int[] s, int plaintextLength) {
    int i = 0;
    int j = 0;
    int[] k = new int[plaintextLength];
    for (int x = 0; x < plaintextLength; x++) {
        i = (i + 1) % 256;
        j = (j + s[i]) % 256;
        App.Utils.swap(s, i, j);
        int t = (s[i] + s[j]) % 256;
        k[x] = s[t];
    }
    return k;
}

The encrypt / decrypt methods are then used to XOR back-and-forth between plaintext and ciphertext.

public int[] encrypt(byte[] plaintextBytes, int[] keystream) {
    // For consistency w. state array and keystream we convert from signed bytes [-128, 127]
    // to unsigned bytes [0, 255] represented as integers.
    int[] plaintextUnsignedBytes = new int[plaintextBytes.length];
    for (int i = 0; i < plaintextBytes.length; i++) {
        plaintextUnsignedBytes[i] = plaintextBytes[i] & 0xFF;
    }


    // XOR the plaintext bytes with the keystream to get the ciphertext
    int[] encryptedData = new int[plaintextUnsignedBytes.length];
    for (int i = 0 ; i < plaintextUnsignedBytes.length; i ++) {
        encryptedData[i] = plaintextUnsignedBytes[i] ^ keystream[i];
    }
    return encryptedData;
}

public String decrypt(int[] encryptedData, int[] keystream) {
    // XOR the ciphertext bytes with the keystream to decrypt back to plaintext
    int[] decryptedData = new int [encryptedData.length];
    for (int i = 0 ; i < encryptedData.length; i ++) {
        decryptedData[i] = encryptedData[i] ^ keystream[i];
    }

    byte[] decryptedBytes = new byte[decryptedData.length];
    for (int i = 0; i < decryptedData.length; i++) {
        // Casting to byte gets rid of all higher-order bits (i.e. anything past fist 8 bits)
        // since byte is a signed type we "wrap around": if decryptedData[i] == 128 then decryptedBytes[i] = -128
        decryptedBytes[i] = (byte)decryptedData[i];
    }

    return new String(decryptedBytes, StandardCharsets.UTF_8);
}

To test the implementation I used the reference implementation of RC4 as provided by CyberChef to generate some known outputs (ciphers) given known inputs (predefined key and plaintext).

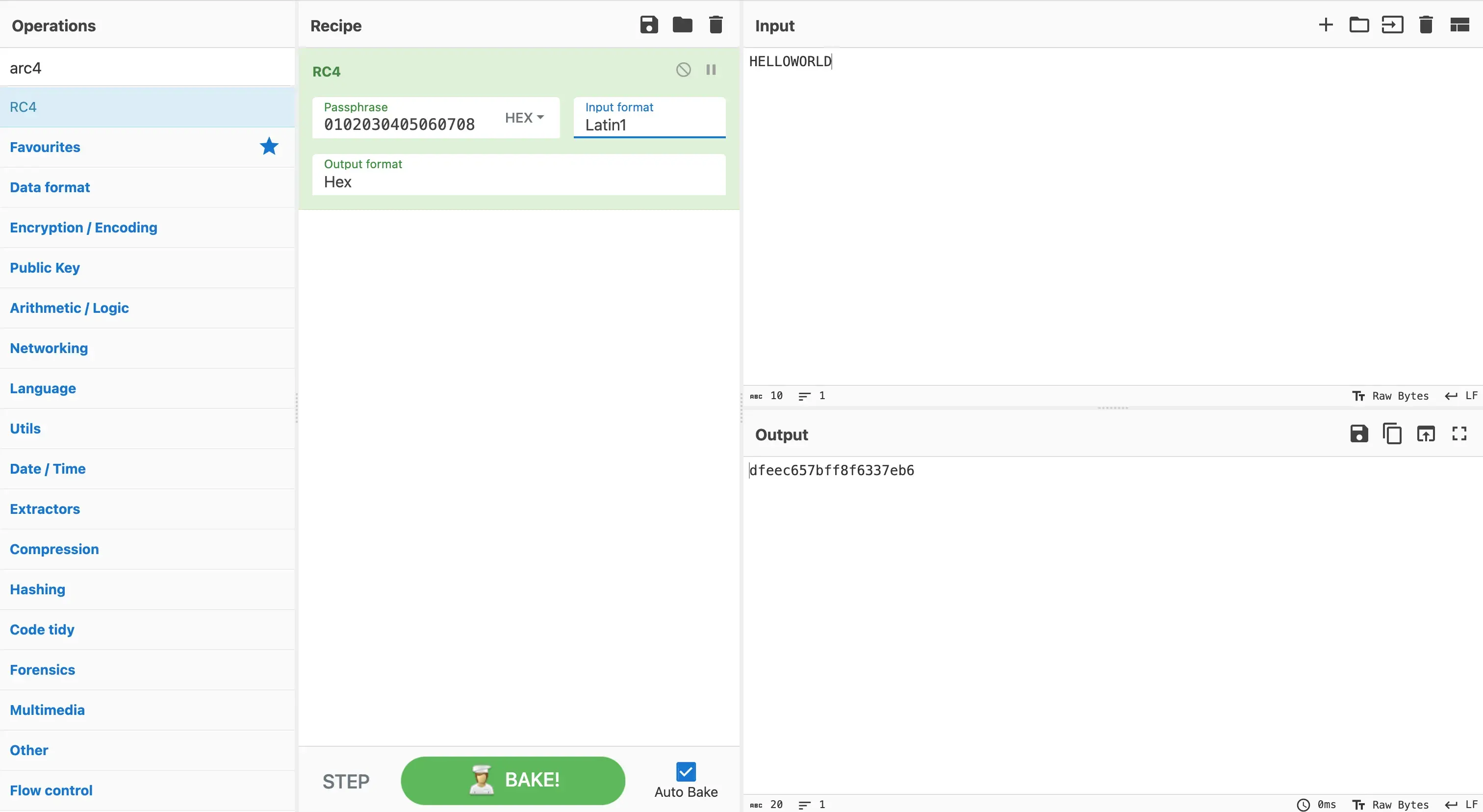
I added some unit tests for both single- and multibyte encodings as well:

    @Test
    public void single_byte_encoding_plaintext_encodes_correctly()
    {
        int[] key = new int[] {1, 2, 3, 4, 5, 6, 7, 8};
        byte[] plaintextBytes = "HELLOWORLD".getBytes();
        Rc4Cipher cipher = new Rc4Cipher(key, key.length);
        ...
    }

    @Test
    public void multi_byte_encoding_plaintext_encodes_correctly()
    {
        int[] key = new int[] {1, 2, 3, 4, 5, 6, 7, 8};
        byte[] plaintextBytes = "HALLÅVÄRLDEN".getBytes();
        Rc4Cipher cipher = new Rc4Cipher(key, key.length);
        ...
    }

Issues with RC4

RC4 and its associated problems has been thoroughly researched. A key theme in the various vulnerabilities is that of correlations between the key chosen to generate the pseudo-random keystream and the resulting cyphertext. Ideally, a cryptographic algorithm should be designed such that it is not possible to discern any patterns or correlations (statistical relationship) between the key’s bytes and the bytes in the ciphertext. However, based on my understanding, the core issue with RC4 is that such correlations were discovered and that feasible attack patterns exploiting these correlations could be developed. The following is some of the findings.

In september 1995, approximately a year after the RC4 code had been reverse-engineered on the cipherpunk mailing list, Roos (1995) discovered a set of “weak keys”[^2]. When these keys are in use, it is possible to predict the first byte of the ciphertext with higher probability.

Given an RC4 key K[0]..K[N] with K[0] + K[1] == 0 (mod 256), there is a

 significant probability that the first byte generated by RC4 will be
 K[2] + 3 (mod 256).
 - Andrew Ross, Weak Keys in RC4, 1995

Ross goes on to state how this could possibly be exploited: Attackers performing a brute-force attack trying to find the right key to reverse some ciphertext could look for the above pattern in the ciphertext. If identified they know that with a higher probability one of the “weak keys” is used an so they can also reduce their search space.

After Ross’ initial paper researchers continued analysis of RC4, Fluhrer, Mantin, and Shamir (2001)[^4] identified an “invariance weakness” in RC4 as well as an attack that was applicable to encryption systems with a mode of operation that was common for multiple commercially deployed systems such as WEP (Wired Equivalent Privacy)

We will show that if the same secret key is used with numerous different initialization vectors and the attacker can obtain the first word of RC output corresponding to each initialization vector he can reconstruct the secret key with minimal effort - (Fluhrer, Mantin, Shamir., Weaknesses in the Key Scheduling Algorithm of RC4, 2001).

Research has progressed since then to establish several feasible attack patterns threatening a growing list of protocols. For example the Bar Mitzvah attack (Hacker Intelligence Initiative, 2015)[^4], where a feasible attack was designed for the TLS/SSL protocol.

Footnotes

[^1]Rescorla, E. (2018). The Transport Layer Security (TLS) Protocol Version 1.3 (RFC 8446). Internet Engineering Task Force (IETF). https://www.rfc-editor.org/info/rfc8446 [^2]Roos, A. (1995, September 22). A class of weak keys in the RC4 stream cipher [Blog post]. Marcel Waldvogel. Retrieved from [URL of the blog post] [^3]Fluhrer, S., Mantin, I., & Shamir, A. (2001). Weaknesses in the Key Scheduling Algorithm of RC4. In Selected Areas in Cryptography, 2259, 1-24. [^4]Hacker Intelligence Initiative. (2015). Attacking SSL when using RC4: Breaking SSL with a 13-year-old RC4 Weakness. Imperva, Inc. https://www.example.com/attacking-ssl-rc4